Conversão de Binário, Octal e Hexadecimal para Decimal
Por Guilherme Lawless para o Pplware
Em tempos um leitor lançou-me o desafio para escrever uns artigos sobre os sistema de representação numérica (sistemas de numeração). Nos sistemas digitais/computação é frequente recorrer-se a diferentes sistemas de numeração para proceder à representação da informação digital.
O sistema de numeração decimal (ou na base 10), que usa dez algarismos é sem duvida o sistema mais utilizado por seres humanos e o sistema binário é o mais frequente no mundo da computação, apenas são utilizados os valores 0 e 1 (pois facilita a representação de tensões), no entanto, existem outros como o sistema de numeração Octal, Hexadecimal, entre outros.
Depois da apresentação dos sistemas de numeração Decimal, Binário, Octal e Hexadecimal, e de já termos ensinado a converter de Decimal para Binário, Octal e Hexadecimal hoje vamos aprender a fazer o inverso, ou seja, de Binário, Octal e Hexadecimal para Decimal.

Binário para Decimal
A conversão do sistema binário para decimal é bastante simples, e baseia-se na aplicação da seguinte fórmula:
Em que:
- bi é o algarismo em binário na posição i, sendo a posição 0 à esquerda da vírgula
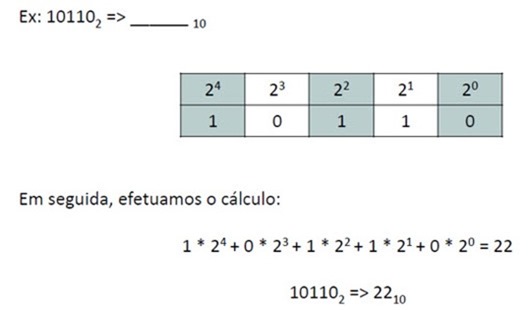
- Com um exemplo, torna-se ainda mais claro a sua utilização. Tome-se então o número não inteiro
Basta então seguir os seguintes passos:
- 1) Começar na primeira posição à esquerda da vírgula.
- 2) Indo para a esquerda, multiplicar cada algarismo por 2i sendo i a sua posição em relação à posição 0
- 3) Caso o número seja inteiro, passar para o passo 4. Neste passo, segue-se a lógica do passo 2, mas para a direita da vírgula. A posição imediatamente à direita é –1
- 4) Finalmente, por aplicação da fórmula, obtém-se o mesmo nº em representação decimal a partir da soma de todas as parcelas calculadas:
A aplicação desta fórmula é intuitiva e faz sentido, pois como já aprendemos anteriormente, cada algarismo em binário tem um valor correspondente na representação decimal.
Exemplo
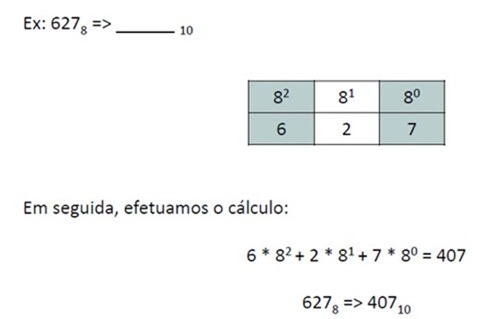
Octal para Decimal
A conversão do sistema octal para o sistema decimal é em tudo semelhante à conversão de binário para decimal, com exceção do valor 2 na fórmula, que passa a 8.
Exemplo
Como já foi aplicado um método muito parecido, vou deixar o desafio ao leitor de tentar converter os seguintes números:
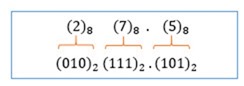
Nota: A conversão octal=>decimal pode ser transformada numa conversão binário=>decimal. Para tal, é necessário converter individualmente cada algarismo em octal para binário. Segue um exemplo, para o número (27.5)8
Obtém-se então, em representação binária, ![]()
Agora basta apenas aplicar o método da conversão binário=>decimal.
Hexadecimal para Decimal
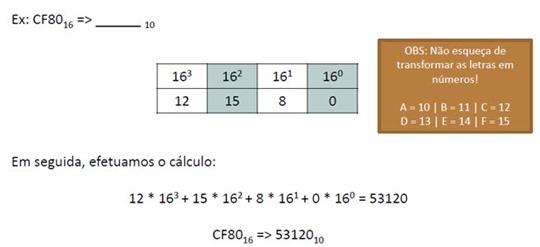
Como seria de esperar, também nesta conversão verifica-se uma parecença com as anteriores. A fórmula a aplicar será:
O método a aplicar é também semelhante aos anteriores, bastando somar as várias parcelas, constituídas pela multiplicação de cada algarismo na posição i (em relação à posição 0, que é à esquerda da vírgula) por 16i
No entanto, é também possível transformar esta conversão numa conversão octal=>decimal ou ainda numa binário=>decimal, consistindo apenas na conversão de cada algarismo hexadecimal no correspondente do sistema de representação pretendido.
Exemplo
A conversão de hexadecimal foi explicada aqui
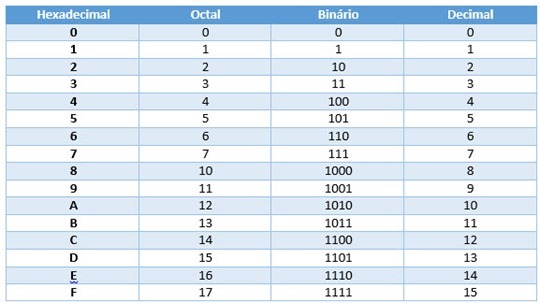
E segue a seguinte tabela:
Em Resumo…
- Conversão Binário > Decimal - Multiplicar o algarismo do número binário pela base elevada ao expoente da sua posição no número
- Conversão Octal > Decimal - Multiplicar o algarismo do número octal pela base elevada ao expoente da sua posição no número
- Conversão Hexadecimal > Decimal - Multiplicar o algarismo do número hexadecimal pela base elevada ao expoente da sua posição no número
Este artigo tem mais de um ano

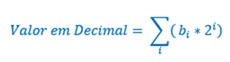



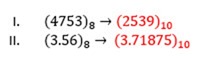






















Parabens pplware! Pena que ja aprendi isso quando estudava! Mas ate ao aprender poça… 😀 Mas aqui é muito mais simples e mais facil aprender! Uma boa aula sim senhor!
Nóe
Para o ano já uso estes tutoriais para dar aula hehehe
Créditos para o Guilherme Lawless 😉
Nada de plagiar Sr. Professor eheh
Cumps
Muito bom, didático e interessante o tutorial. Parabéns!
Uma observação: No item 3.b (Binário para Decimal), não seria 1 ao invés de 0 ?
Sim, sem dúvida! Obrigado pela correção 🙂
Estou a aprender agora… E fiquei com a mesma dúvida nesse passo 3!
Se está errado, é possível escrever o certo??
O correto é:
b) 1 x 2ˉ² = ͟1͟ = 0,25
2²
Desculpe, o 2² é para ficar embaixo do ̲1̲ .
Desculpe, o 2² é para ficar embaixo do ̲1̲ .
Zero sempre vai da zero
Lindos Tutorias.
no exemplo do octal para decimal, eu fiz a conta e sempre da 400, não entendi porque deu 407, poderia me explicar?
Oi Beatriz,
a conta será (6 * 64)+ (2 * 8) + (7 * 1) = 407
8**2 = 64, 8**1 = 8 e 8**0 = 1
espero ter ajudado.
Boas,
calculadoras que efetuem cálculos com vírgula flutuante existem?
no passo 3 b) o coeficiente será 1 em vez de 0.
Abraço
Muito boa a explicação. Melhor do que as dos livros que estava estudando. Parabéns!
em binario para decimal no passo 3 ta como 0*2-²= 1/2²= 0,25
em vez de 1*2-²=1/2²=0,25. Mas muito bacana este site.
Muito útil parabéns.
Mas penso que poderiam colocar mais conversões
Ex binário – hexadecimal.
Obrigado
Melhores cumprimentos Hugo Abreu.
deveria ter octal para binários e como resolver questoes com números muito grandes
ola
eu não entendi a Nota no passo do Octal, no exemplo de Decimal>Binário por que 27.5 = 010111.101 ?
de 27.5 tu usa o multiplicador de 26 no caso pra poder dar mais certo o calculo e nao colocar o 010111.101 :/
Adoreiiiiii
isso xta bm resumido
Muito obrigado, explicacao objectiva.