GeoGebra 3.2 – A simplicidade da Geometria!
Hoje trago uma aplicação bastante utilizada por quem utiliza a geometria dia-a-dia. Quer seja na escola ou no trabalho, o GeoGebra é sempre um programa útil para se ter connosco.
Provavelmente já ouvir falar ou até já experimentou o GeoGebra, mas nunca sentiu necessidade de o obter. De facto, esta é uma aplicação bastante útil para diversas situações, mas é especialmente útil para estudantes. Com o GeoGebra podem pôr em prática diversos conhecimentos de geometria e depois, por exemplo, colocar o gráfico obtido num trabalho escolar ou relatório.
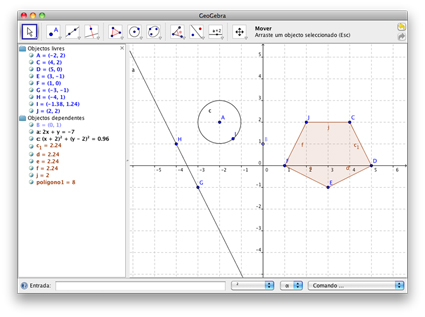
As opções do GeoGebra são bastantes e de fácil uso. Pode colocar pontos no referencial, criar uma recta a partir de dois pontos, colocar uma circunferência, polígonos, (...) no referencial, ... As opções são vastas.
Umas das vantagens do GeoGebra é o seu aspecto intuitivo e simples que facilitam todo o trabalho. Uma das minhas funções favoritas é lista do lado esquerdo que nos mostra as coordenadas dos pontos que inserimos no referencial, bem como as equações das rectas. Esta característica é bastante útil para cálculos em exercícios e problemas.
Resumindo, o GeoGebra é uma ferramenta bastante útil para estudantes, e não só, e o melhor de tudo: está disponível para Mac, Windows e Linux.
![]() Licença: Freeware
Licença: Freeware
![]() Sistemas Operativos: Mac / Windows / Linux
Sistemas Operativos: Mac / Windows / Linux
![]() Download: GeoGebra 3.2
Download: GeoGebra 3.2
![]() Homepage: GeoGebra
Homepage: GeoGebra
Este artigo tem mais de um ano
























Excelente dica!
Obrigado.
Isto agora é programas para tudo XD
Ou faço geometria rápida e simples em segundos…
Só programas. programas, programas…
Eu usava um bem mais complexo nas aulas de matematica que nao me recordo do seu nome, mas creio que era pago, este por acaso desconhecia completamente, pena é agora não percisar de “brincar” com este tipo de programas 😀
Isto é fixe e lembrou-me uma cena…
há algum programa para fazer de calculadora grafica??
wxMaxima é o que se usa na FEUP, faz mais que uma máquina grafica e bem mais rápido, depois de perceberes como funciona. BTW usa o Help do maxima que lá diz tudo.
http://www.torrentreactor.to/torrents/view_1286940/Virtual_TI_83_Graphing_Calculator_Emulator_ROM.html
magnet:?xt=urn:btih:3d4cf9938d14f5ae5e12507ee87b426df83de6c8&dn=Virtual+TI+Graphing+Calculator+&tr=http%3A%2F%2Fdenis.stalker.h3q.com%3A6969%2Fannounce
Este funciona perfeito testei. para sacar este usei o utorrent. Aparece uma TI – 83 no ecran e depois é só carregar nos botões com o rato. Está muito bem feita.
Dá muito jeito nas aulas para mostrar gráficos, propriedades das figuras geométricas e demonstrações, como a do teorema de Pitágoras, etc.
Olá
Por estranho que pareça, ou coincidência, amanhã na escola vou ter uma formação para a utilização do GeoGebra em substituição do Geomethers SketchPad.
Este programa dá para trabalhar a partir do sistema de projecções divididas pelo eixo x?
Deixa me aproveitar que está malta ligada as geometrias 🙂 e fazer uma pergunta.
Alguem sabe que feramenta (preferencialmente opensource) para resolver o problema de “CUTTING STOCK” (cortar uma barra em muitas medidas com o minimo desperdicio) unidimensional.
Andei a procura e n encontrei nada k me satisfiesse…
Aceito qualquer coisa… programa … funcões em C, VB, Excel, Python, …… anything
(ja estou farto de fazer fichas de corte a mão)
🙂
O que sei:
This is an LP (Linear programming) problem with the complication that the number of different ways to cut each stock piece grows exponentially with the number of lengths required and may get too large for traditional LP techniques
O que não sei:
WTF is a “LP problem” ???
Boa noite Diego,
LP significa Linear Programing ou seja programação linear. Não tem nada a ver com uma linguagem de programação (pelo menos no imediato) e sim com disciplinas/áreas de investigação operacional (matemática aplicada or vezes bastante avançada).
Para resolução de problemas de Investigação Operacional existem muitos algorítmos e heurísticas (soluçoes de compromisso) de onde o mais afamado se denomina simplex (e sim não tem nada a ver com o Simplex do nosso Engº primeiro) revela-se algo bastante mais estimulante.
Trata-se de uma área muito vasta e com imensas aplicações à realidade por exemplo os sites do google maps, via-michelin, os GPS dos carros, utilizam destes algorítmos mais concretamente para cálculo de caminhos mais curtos recorrendo a teoria dos grafos.
Por último é uma área muitíssimo ligada à computação uma vez que quando se passa do campo teórico das aulas para aplicabilidade à realidade dificilmente se conseguem resolver os problemas sem cálculo computacional e sem por vezes ter que implementar os algorítmos com recurso a linguagens de programação.
Há uns 7 anos talvez lhe conseguisse sugerir um algorítmo ou formalizar o problema hoje já estou bastante esquecido. Mas em resumo um LP Problem é um problema que tem uma função objectivo f(x, y, z, …)
que se procura minimizar ou maximizar sujeita a determinadas restrições. Tratando-se de um problema LINEAR essas restrições são rectas (ou planos no espaço) que, ao intersectarem-se definem um conjunto de soluções admissíveis do qual (tendo o problema solução) pelo menos um é o ponto óptimo (ou seja um (x, y, z, …) que maximiza ou minimiza a função objectivo).
A investigação operacional faz uso de algorítmos e métodos numéricos para optimizar em contraponto a análisa matemática faz uso de métodos analíticos, 1ª derivada (ou gradiente), 2ª derivada (ou hesseana), pontos de inflexão etc. O problema é que nem sempre se conseguem calcular as derivadas…
Com esta dissertação a ver se cativo mais uns curiosos para as áreas ciêntificas de que tanto este pais necessita.
Confirmo-lhe ainda que muitos problemas de investigação operacional têm soluções complexas e nem têm algorítmos para obter o óptimo (têm apenas heurísticas) e com um nome semelhante a Cutting Stock lembro-me do problema KnapSack (saco mochila) que segundo me vem à memória não era nada simples…
Trata-se de optimizar a colocação de objectos com medidas num determinado espaço (uma mochila com um determinado volume)
Tem aqui uma ideia da coisa
http://en.wikipedia.org/wiki/Cutting_stock_problem
Trata-se de um Problema de Prgramação Linear Inteira que é bem mais complexo que um problema de Programação Linear porque as soluções só podem ser número inteiros.
Tipicamente estes problemas resolvem-se com o Branched Simplex ou seja (com imensas tentativas utilizando o simplex)
Bom Dia ANtonio Lopes
Muito Obrigado pelas dicas e pelo chuto na direcção certa 🙂
Lembro me na universidade deste problema da mochila (mas este sim era muito complexo pois cada objecto tinha um volume e um lucro (ou valor)) e o crescimento do calculo nescessario era logaritmico.
Eu ja tinha uma ideia de como resolver o problema, mas é demasiado trabalhosa (para mim e para o PC 🙂 ) que era testar tods as possibilidades e escolher a melhor… anular as medidas aproveitadas e refazer o processo para as que sobram…. mas tendo eu muitas vezes 5.000 medidas…. a coisa pode ficar brutal e depois ao testar o algoritmo (fiz em python) tinha serias dificuldades em saber se tinha errado e estava num loop infinito ou se deveria esperar 🙂
E esta solucão (a minha) é uma solução burra (a bruta)….
Vou estudar “Branched Simplex” à ver se resolvo o problema.
Mais uma vez MUITO OBRIGADO
Olá Diego,
O algoritmo chama-se julgo branch and bound pois vai criando uma árvore de decisão em que cada ramo acaba por ser uma iteracção do simplex. Mas há mais algoritmos para resolucao de Problemas de Programação Linear Inteira. De qualquer forma com o poder computacional dos dias de hoje pode por vezes revelar-se mais rápido implementar “à bruta” e testar todas as combinaçõs possíveis. Sugiro-lhe que utilize uma linguagem de mais baixo nível tipo c++ para contruir estruturas tipo árvores binárias e listas ligadas e iterar sobre elas (ou mesmo hash-tables). Em alternativa para criar todas as combinações possíves pode também efectuar produtos cartesianos entre tabelas de uma base de dados e depois testar cada uma das combinações individualmente. Etc.. são só ideias.
EU NAO SEI O QUE EST MAS GOSTAVA DE SEBER