Conversão Decimal para Binário, Octal e Hexadecimal
Na semana passada um leitor lançou-me o desafio para escrever uns artigos sobre os sistema de representação numérica (sistemas de numeração). Nos sistemas digitais/computação é frequente recorrer-se a diferentes sistemas de numeração para proceder à representação da informação digital.
O sistema de numeração decimal (ou na base 10), que usa dez algarismos é sem duvida o sistema mais utilizado por seres humanos e o sistema binário é o mais frequente no mundo da computação, apenas são utilizados os valores 0 e 1 (pois facilita a representação de tensões), no entanto, existem outros como o sistema de numeração Octal, Hexadecimal, entre outros.
Depois da apresentação dos sistemas de numeração Decimal, Binário, Octal e Hexadecimal hoje vamos aprender como converter de Decimal para os outros sistemas de numeração.

Conversão Decimal > Binário
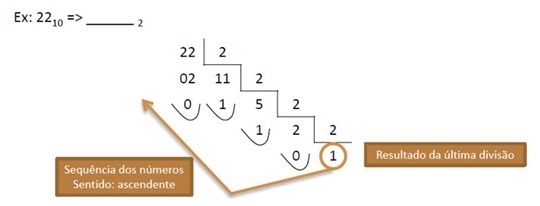
A conversão de decimal para binário (ou seja da base 10 para a base 2), consiste em dividir progressivamente o valor decimal por 2, obtendo-se um resultado e um resto. De referir que o resultado em cada iteração terá sempre o valor de 0 ou 1. Deve-se dividir o número até que o quociente da divisão seja igual a 0 (zero).
Depois de finalizado o calculo, basta agrupar todos os valores (ou seja, os restos de cada iteração) de baixo para cima.
Resultado: 22 (10) > 10110 (2)
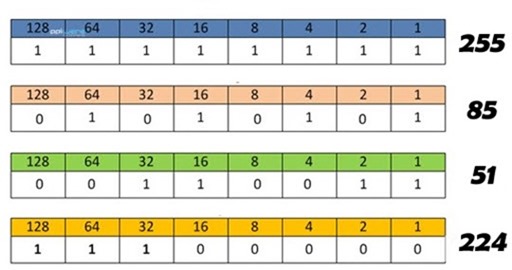
Outra forma desta conversão (mais prática) é usando informação da tabela CIDR e atribuindo pesos às potencias de 2. Exemplo para valores até 255.
Conversão Decimal > Octal
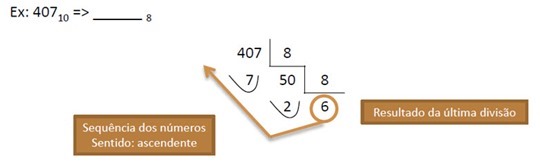
A conversão de decimal para octal (ou seja da base 10 para a base 8), consiste em dividir progressivamente o valor decimal por 8, obtendo-se um resultado e um resto. De referir que o resultado em cada iteração terá sempre um valor menor que 7.
Tal como no exemplo anterior, depois de finalizado o calculo, basta agrupar todos os valores (ou seja, os restos de cada iteração) no sentido ascendente.
Resultado: 407(10) > 627(8)
Conversão Decimal > Hexadecimal
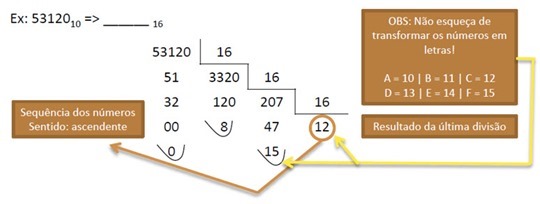
A conversão de decimal para hexadecimal(ou seja da base 10 para a base 16), consiste em dividir progressivamente o valor decimal por 16, obtendo-se um resultado e um resto. Não esquecer que o sistema hexadecimal utiliza os símbolos: 0,1,2,3,4,5,6,7,8,9 do sistema decimal e as letras A,B,C,D,E,F.
(Equivalências:A=10,B=11,C=12,D=13,E=14eF=15)
O resultado da conversão deverá ser também obtido, reunindo o valor dos restos, no sentido ascendente.
Resultado: 53120(10) > CF80(16)
Num próximo artigo iremos ensinar a proceder à conversão de octal, binário e hexadecimal para decimal numeração. Espero que tenham gostado desta explicação e apenas deixar um obrigado para o Leandro Costa, que disponibilizou publicamente uma apresentação no slideshare e de onde foram aproveitados alguns esquemas. Desde já convidamos os leitores que estejam interessados em colaborar com esta rubrica, que enviem um e-mail para o nosso endereço geral.
Este artigo tem mais de um ano






















Muito bem explicado!
Gráficos bastante descritivos e com as pricipais observações. Bom trabalho mesmo!
és um gamer
Boa tarde!
O artigo está muito bem escrito, de forma sucinta e eficiente! (Apesar de não ter percebido a conversão mais prática do decimal para o binário…).
Também poderiam explicar o sistema vigesimal (base 20)? Não sei se tem alguma praticabilidade. Apenas sei que era o sistema usado pelos Maias nos seus cálculos matemáticos em Astronomia, com uma pequena margem de erro aos que fazemos actualmente!
Parabéns pelo vosso trabalho!
Escelente post, amanhã até vou ter uma formação com membros da Schneider Electric e vou precisar disto, mesmo a calhar, já me deu umas ideias…
Obrigado e bom trabalho a toda a equipa
22/11=2
Não tem resto…
Quer dizer, 22/2=11, sem resto.
Velhos tempos em que o decimal->hexadecimal->decimal era usado todos os dias. Dois exemplos hexa:
6ab3f2 + 5c2e19 = c6e20b
6ab3f2 – 5c2e19 = 0e85d9
Sou inocente diante desta relação que mencionou acima, poderia bondosamente explicar-me sobre isso, despertou a minha curiosidade senhor Valente, quero aprender também como senhor também já teve essa oportunidade um dia.
Sou inocente diante desta relação que mencionou acima, poderia bondosamente explicar-me sobre isso, despertou a minha curiosidade senhor Valente, quero aprender também como senhor também já teve essa oportunidade um dia.
Muito bem explicado, sim senhor.
Muito legal essa explicação, entretanto eu acharia interessante colocar os créditos ao professor Leandro Costa Coelho pois acredito que essa foi a fonte do material aqui publica (pelo menos em partes) e o autor merece seu crédito. De qualquer maneira friso que a explicação foi muito boa.
Isto é brutal já á muito que quero ir para engenharia informatica pelo simples facto de gostar bastante de computadores,telemoveis,etc. Mas agora ainda tenho mais vontade… Eu ainda só estou no 12o ano e o meu unico medo(espero que seja só este) é mesmo a parte da fisica… Já agora alguem me pode explicar porque é que 2+2=11?
em que sistema te baseias para dizer que 2+2=11?
em relação ao artigo 2+2(dec)=100(bi)=4(oct)=4(hex)
Valeu amigo, com essa explicação consegui fazer os algoritmos em Java para realizar as conversões. É bem simples, exceto pelo hexadecimal devido as letras, nada que um switch no while resolva. Obrigado.
Muito bem Explicado, espero que outras pessoas também aprendam oque eu aprendi.
Excelente explicação!
Parabéns!!!
valeu, mesmo!
estou a seguir engenharia de informática e as dicas que deixaste me fizeram entender melhor.
boa explicação…
gostei. obrigado
Não tem uma maquina convertora
Boas, nao consigo perceber como se obtem o valor do resto na conversão para heximal.. Alguém poderia explicar?
Gostei
Como resolvo esas equações aqui:
a) (11101011101.0101)2 = ( ? )10 = ( ? )4
b) (65070875.0568)9 = ( ? )3
c) (6756376)8 = ( ? )5
d) (DAECD8.AEF7)16 = ( ? )8
e) (330213102.0330221)4 = ( ? )8
Isso é coisa leve
Good
Muito bom!
Ok. .
Muito bom, Vlw
Muito bom . Fiquei esclarecida e foi a primeira vez que fiz esta conversão
Boa explicação, gostei imenso!
Valeu apena!Chumbo Grosso Enterprise®
Foi muito útil, pois vi isso há muito, precisava relembrar algumas coisas…
Queria em primeiro agradecer, valeu mesmo, eu nao conseguia assistir as aula, por isso n conseguia compreender os exercicio , mais com essa explicaçao tdo fico bem claro valeu mesmo continua .. Há eu quero as proximas continuacao tambem
muito interessante, porém queria saber como se faz a conversão do binário, octal ou hexadecimal para o decimal.